バイナリの読み方

バイナリの読み方を学ぶことに興味がある場合は、その方法を理解することが重要です。 2進数 仕事。

2進数は、「基数2」の記数法として知られています。つまり、各桁に2つの可能な番号があります。 1または0。 2進数に1または0を追加することにより、より大きな数値が書き込まれます。

2進数を理解する

バイナリの読み方を知ることは、コンピュータを使用する上で重要ではありません。 しかし、コンピュータがどのように保存するかをよりよく理解するために、概念を理解することは良いことです メモリ内の数値. また、16ビット、32ビット、64ビットなどの用語や、次のようなメモリ測定値を理解することもできます。 バイト （8ビット）。

バイナリコードの読み方

バイナリコードを「読み取る」とは、通常、2進数を10進数（10進数）に変換することを意味します。 この変換は、バイナリ言語がどのように機能するかを理解すれば、頭の中で実行できるほど簡単です。b。

2進数の各桁の位置は、桁がゼロでない場合、特定の値を持ちます。 これらの値をすべて決定したら、それらを合計して、2進数の基数10（10進数）の値を取得します。

これがどのように機能するかを確認するには、2進数の11001010を使用してください。

1. 2進数を読み取る最良の方法は、右端の数字から始めて、左に向かって進むことです。 その最初の場所の累乗はゼロです。つまり、その桁の値は、ゼロでない場合は、2の0乗または1の累乗です。 この場合、桁がゼロであるため、この場所の値はゼロになります。

   

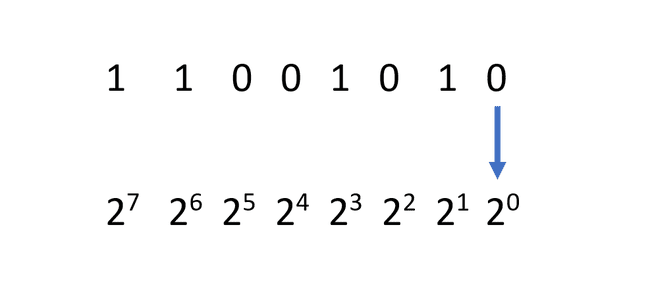
2. 次に、次の桁に移動します。 1の場合は、2の1乗を計算します。 この値もメモしてください。 この例では、値は2の1乗、つまり2です。

   

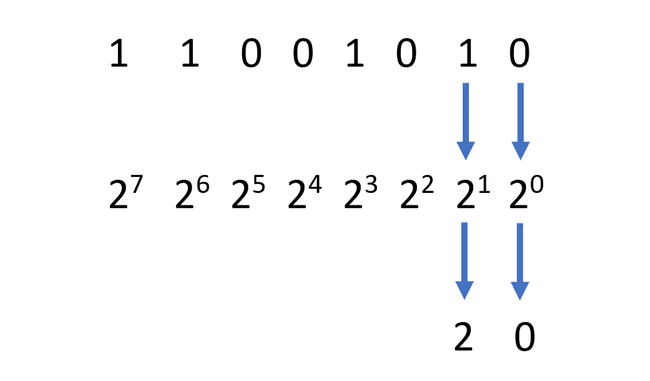
3. 左端の桁に到達するまで、このプロセスを繰り返します。

   

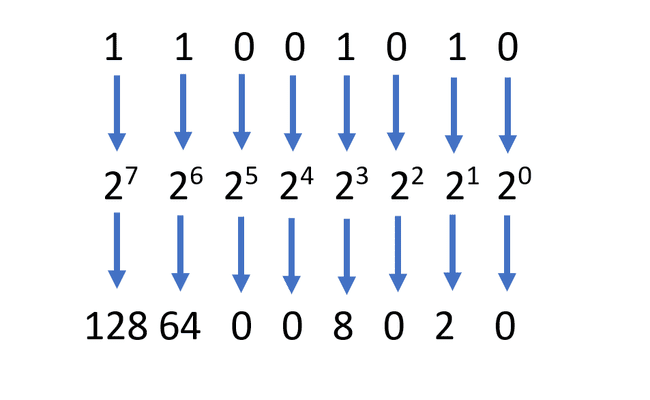
4. 最後に、これらの数値をすべて合計して、2進数の全体的な10進値を取得するだけです。 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 = 202

   このプロセス全体を方程式の形で見る別の方法は次のとおりです。 1 x 2⁷ + 1 x 2⁶ + 0 x 2⁵ + 0 x 2⁴ + 1 x 2³ + 0 x 2² + 1 x 2¹ + 0 x 2⁰ = 202

署名された2進数

上記の方法は、基本的な符号なし2進数に対して機能します。 ただし、コンピューターには、2進数を使用して負の数を表す方法も必要です。

このため、コンピューターは符号付きの2進数を使用します。 このタイプのシステムでは、左端の数字は 符号ビット、残りの桁はマグニチュードビットと呼ばれます。

符号付き2進数の読み取りは、符号なしとほぼ同じですが、わずかな違いが1つあります。

1. 符号なし2進数について上記と同じ手順を実行しますが、左端のビットに到達したら停止します。

   

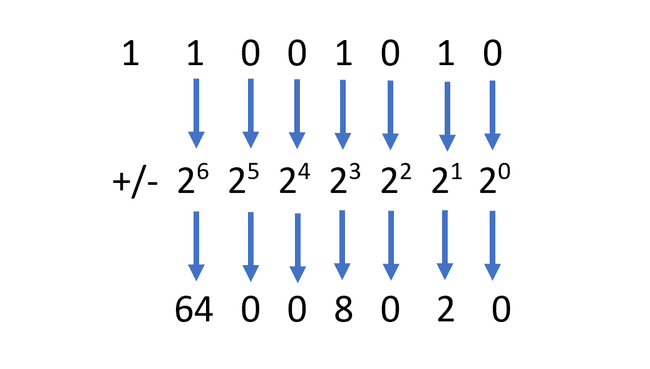
2. 符号を判別するには、左端のビットを調べます。 1の場合、数値は負です。 ゼロの場合、数値は正です。

   

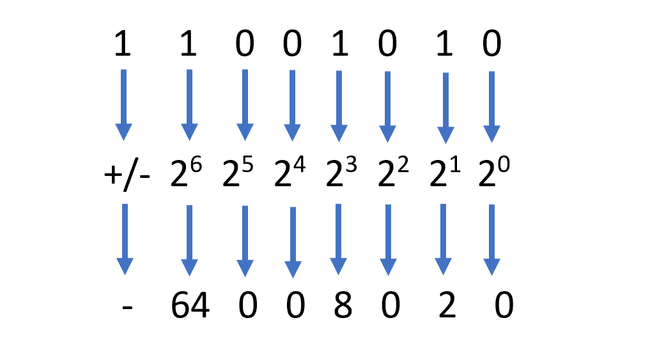
3. ここで、前と同じ計算を実行しますが、左端のビットで示されているように、数値に適切な符号を適用します。 64 + 0 + 0 + 8 + 0 + 2 + 0 = -74

4. 符号付き2進法を使用すると、コンピューターで正または負の数値を表すことができます。 ただし、最初のビットを消費します。つまり、数値が大きいほど、符号なし2進数よりもわずかに多くのメモリが必要になります。